Это простенький алгоритм о нахождениии кратчайшего пути из точки А в точку Б на графе. Давайте рассмотрим сам принцип алгоритма на примере. А с его реализацией, если вам она потребуется, вы справитесь, мы уверены!

Итак, имея следующий граф, мы хотим найти кратчайший пункт из точки A в точку F:

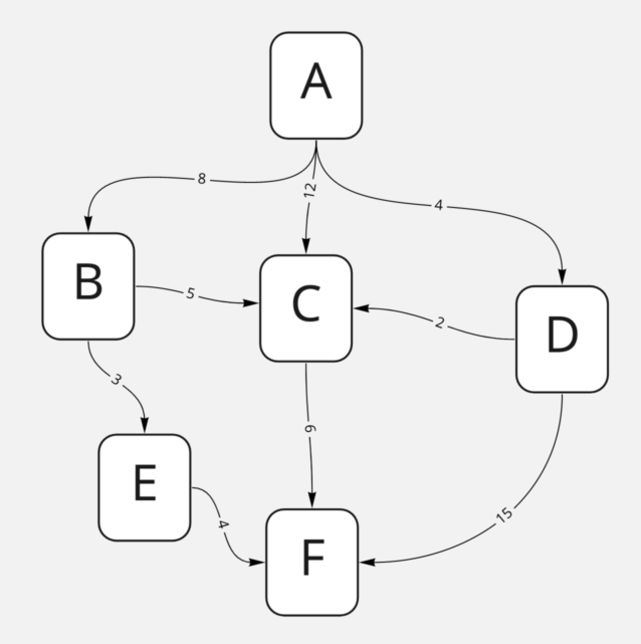
Этот алгоритм — жадный, а значит, он будет искать самый короткий путь нахождением кратчайших путей между всеми нодами. Как ему это удастся? Давайте посмотрим на пару итераций нашего алгоритма. Сначала дойдём из точки A в каждую из нод, до которых мы можем добраться:

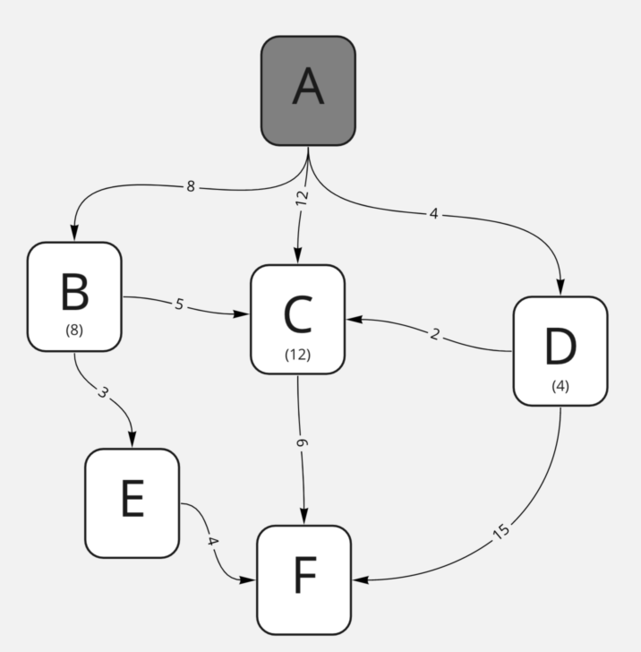
В каждую из нод добавилась информация о том, за сколько до них можно дойти. Давайте сделаем ещё одну итерацию для точки D:

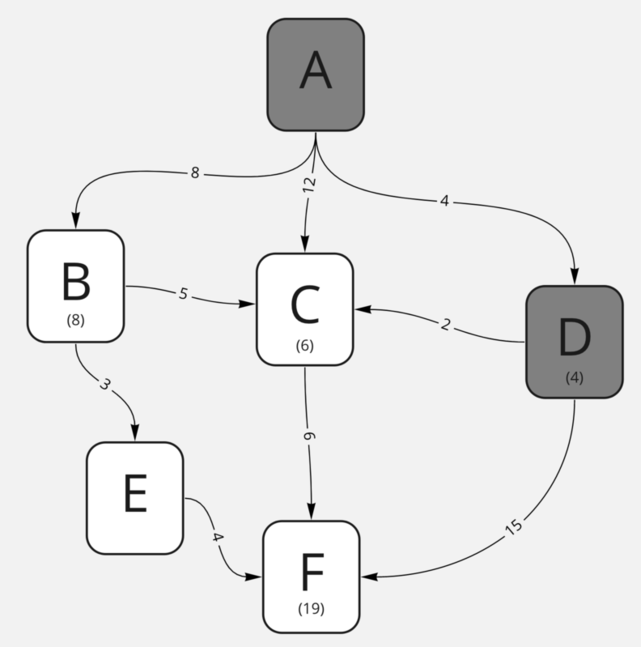
Как мы видим, в точке C обновилась информация о достижимости: теперь мы можем дойти до неё за 6 (за 4 до D из A и за 2 до C), а не за 12! Именно так мы и пройдём все возможные маршруты и найдём кратчайший путь. Давайте объединим итерации с нодами B и C:

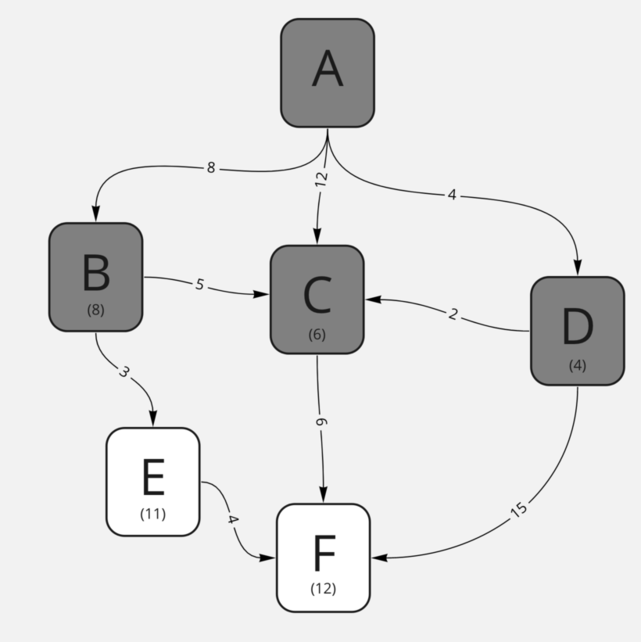
Осталась лишь одна непросмотренная нода — E.

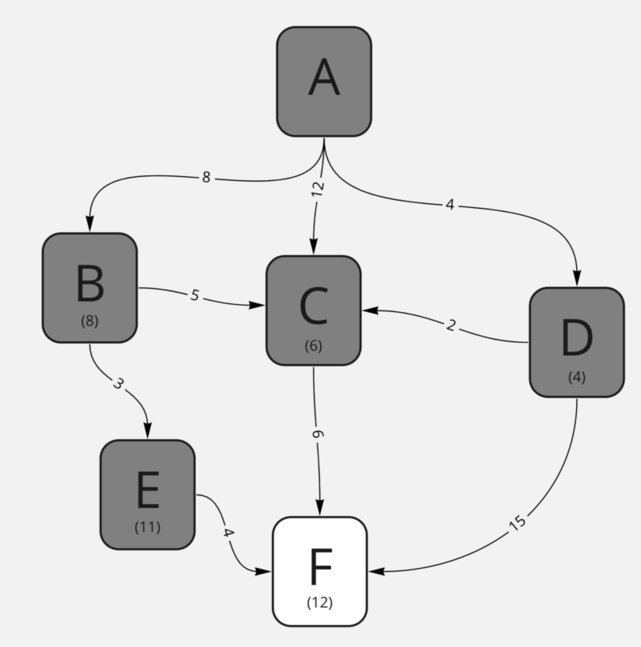
Результат её прохода ни на что не повлияет — мы уже нашли путь в F за 11, а путь из E займёт уже 15. Таким образом, результат работы нашего алгоритма — кратчайший путь A-D-C-F с расстоянием в 12.