Как мы уже узнали, мы не можем просто так хранить в памяти компьютера адреса в виде строк. Поэтому нам нужно каким-то образом преобразовывать наши ключи-строки в обычные индексы для массива. Этим и занимается хеш-функция. Визуализировать это можно примерно так:

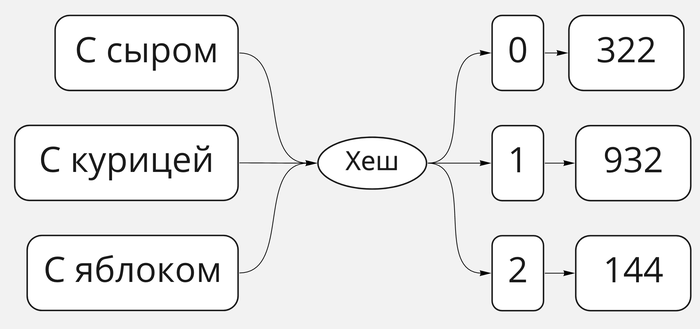
Хеш-функция отображает ключи в индексы массива

То есть она и есть то звено, которое ассоциирует строки с числами. Хорошая хеш-функция должна делать это очень быстро, а также не позволять двум строкам показывать на один и тот же индекс в массиве, поверх которого работает. Напомним, что такие ситуации, при которых это происходит, называются коллизиями.

Давайте посмотрим на пару простых хеш-функций:

Остаток от деления

Это самый простой способ получить из большого числа небольшое: если мы хотим класть численные ключи и они огромны, то мы просто получим остаток от деления на то число, массив какой длины нам «не жалко» отдать под хранение для этой таблицы. Например, вот так:

Простейшая хеш-функция

Сложение строки

Если мы хотим класть в нашу хеш-таблицу ключи-строки, то простой остаток от деления уже не поможет: мы не можем делить строчку на число. Зато вполне себе можем получить из строки число, если представим каждый символ как его положение в таблице символов (с помощью charCodeAt, например), а затем уже взять остаток от её деления. Это добавит ещё одно небольшое промежуточное представление в нашей визуализации:

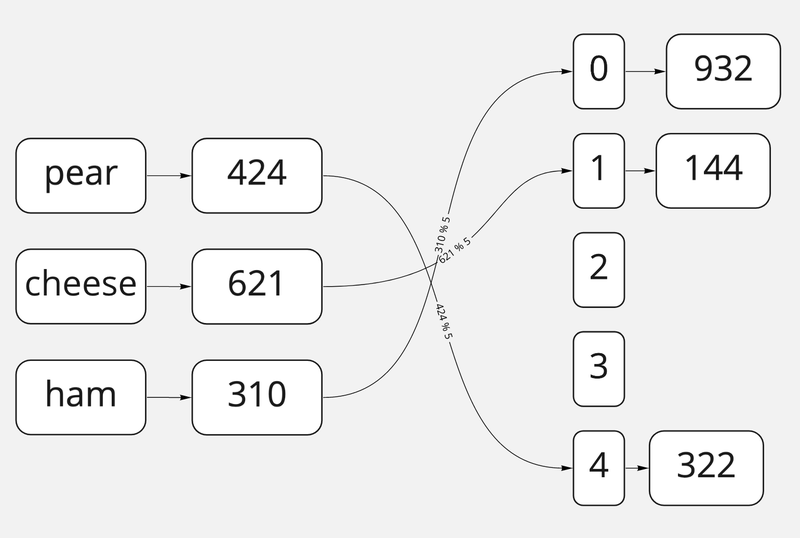
Хеш суммированием строки

Примерно так и работают большинство хеш-функций. Они при помощи каких-то операций получают из объекта число, а затем берут остаток от этого числа либо уменьшают его при помощи других операций. Например, методом «середины квадрата».

«Настоящие» способы хеширования

Конечно, такими слабыми хешами как те, что мы рассмотрели, не пользуются. «Промышленные» алгоритмы хеширования вроде MD5 или SHA-2 гораздо надёжнее и устойчивее к коллизиям, но рассматривать их здесь мы не будем — они слишком сложные для покрытия без достаточной теоретической базы. Если хотите, можете прочитать про них сами — это очень полезно для общего развития.

Коллизии

У первых наших примеров стойкость к коллизиям очень плоха — мы можем положить в первую нашу таблицу что-то по ключу 333, хеш-функция получит остаток от деления на 3 — 0 и перезапишет то, что хранилось раньше по ключу 153.

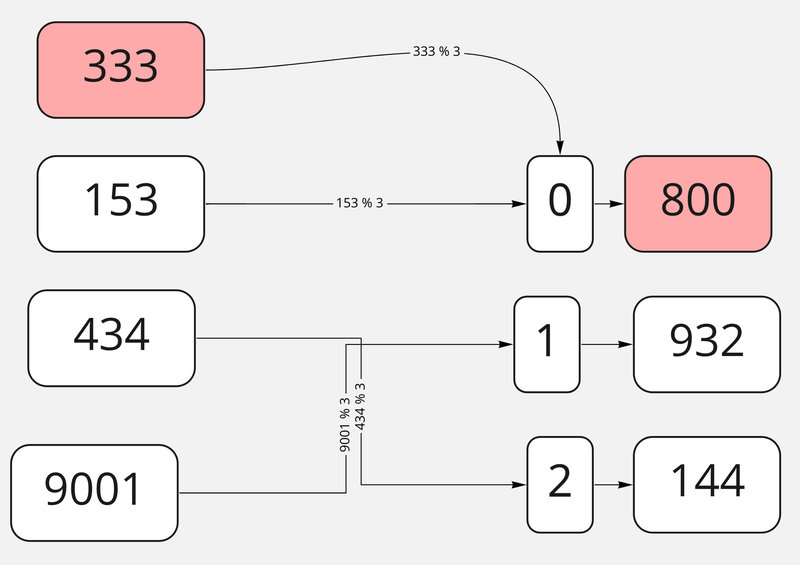
Коллизия!

Как же обрабатывать такие ситуации?

Метод цепочек

Будем хранить значение в массиве, над которым оперирует хеш-функция, вместе с ключом. Как только случится коллизия — просто сделаем из одного элемента связный список, в который положим «цепочку» из элементов с одинаковым хешом. Когда нам надо будет считать данные по ключу, а по его индексу будет лежать такая «цепочка», то нам придётся пройти её в худшем случае полностью, пока мы не найдём нужный нам ключ.

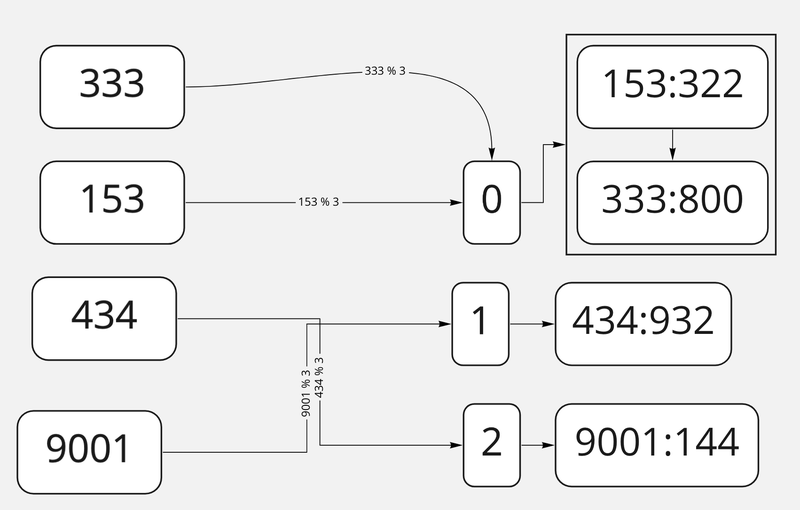
Разрешение коллизий методом цепочек

Если в этом примере мы захотим получить данные по ключам 434 или 9001, для нас эти операции выполнятся настолько же быстро, насколько работает хеш. А вот если мы захотим получить данные по ключу 333, то наткнёмся на цепочку и сначала в ней просмотрим запись по ключу 153, а уже только затем найдём искомый элемент.

Такой метод поможет нам сохранить скорость записи в O(1), но чуть замедлит скорость чтения.

Метод открытой адресации

Мы также будем хранить в массиве вместо простых значений пару ключ-значение, но уже не будем складывать по одному ключу цепочки из данных с одинаковыми хешами. Вместо этого будем отступать от этого элемента на какой-то фиксированный шаг и пробовать записать данные туда (либо считать оттуда, если мы пытаемся что-то найти по ключу). Если это место занято, просто идём на этот же шаг дальше и попробуем записать туда (или считать оттуда) — и так делаем, пока не встретим или пустое место, или то, что мы ищем.

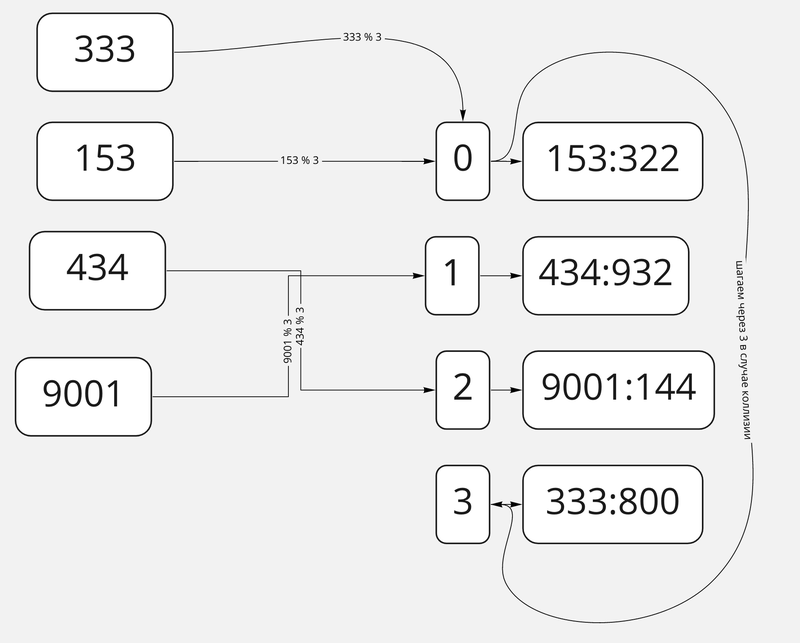
Разрешение коллизий методом открытой адресации

По эффективности этот метод похож на разрешение коллизий методом цепочек. Однако при частых коллизиях наш массив может разрастись довольно сильно и иметь большую разряженность данных на пустоту внутри.

Метод отступа на постоянное количество шагов называется линейным пробированием. Также существует квадратичное пробирование, когда мы начинаем отступать на большее количество шагов с каждым неуспешным попаданием по коллизии, а также двойное хеширование, когда количество шагов помогает вычислить вторая, вспомогательная, хеш-функция.

Рехеширование

Это самая распространённая ситуация, которая приводит к увеличению времени вставки до O(n). Как только случается коллизия, мы просто увеличиваем число, по которому брали остаток, и перекладываем все наши элементы в новую хеш-таблицу. Тогда каждая операция чтения вернётся к сложности в O(1). Зачастую этот метод применяется вместе с двумя предыдущими, когда количество коллизий превышает некий заданный разработчиками коэффициент.

В следующих демонстрациях, наконец, посмотрим на то, какие задачи призваны решать хеш-таблицы! Сами таблицы мы реализовывать не будем — у нас уже есть Map. Теперь вы понимаете, как примерно он работает «под капотом» и почему Map настолько быстр.