Напомним условия нашей задачи. Предположим, вы разрабатываете веб-приложение для загрузки файлов — этакий менеджер загрузок из прошлого. Но из-за ограничений на стороне сервера можете получать данные только пачками по несколько мегабайт в зависимости от местоположения сервера (притом в одной пачке могут лежать части разных файлов). И уже на фронте вы склеиваете их в нормальные файлы. Всё усложняется тем, что все файлы заранее разбиты на части разных размеров. То есть какие-то из них могут быть с частями по 7 МБ, какие-то — по 4 МБ, какие-то — по 5 МБ... Задача состоит в том, чтобы добавить в каждую пачку с сервера столько частей разных файлов, чтобы использовать максимальное количество места из доступного для пачки из 10 МБ.

Давайте с новыми знаниями вернёмся к старой задаче и попробуем решить её оптимально. Как мы узнали из предыдущей статьи, нам нужно попытаться свести задачу к подзадачам, которые связаны между собой. В нашем случае стоит начать решать задачу для меньших пачек данных. А затем, используя их решения, получить решение исходной задачи.

Составим таблицу из всех возможных частей файлов и всех возможных размеров пачки меньше 10 МБ с шагом в один мегабайт:

Теперь начнём заполнять таблицу сверху вниз. Сначала попробуем заполнить строку принятия решений «класть нам часть из 4 МБ или нет». В каждую ячейку будем записывать общий размер получающейся пачки и то, какие части файлов туда пойдут. Заполнить эту строчку довольно просто. В пачки до 4 МБ мы ничего не можем положить. В пачку от 4 МБ до 8 МБ положим одну часть. В более объёмные — две.

На этом этапе важно помнить, что сейчас мы решаем задачу только для частей одного размера, а трогать части из других строк пока не можем. Сейчас мы заняты решением подзадачи, которое будем переиспользовать в других подзадачах для частей большего размера.

Начнём заполнять вторую строчку. Можно предположить, что она заполнится так же, как и в первый раз:

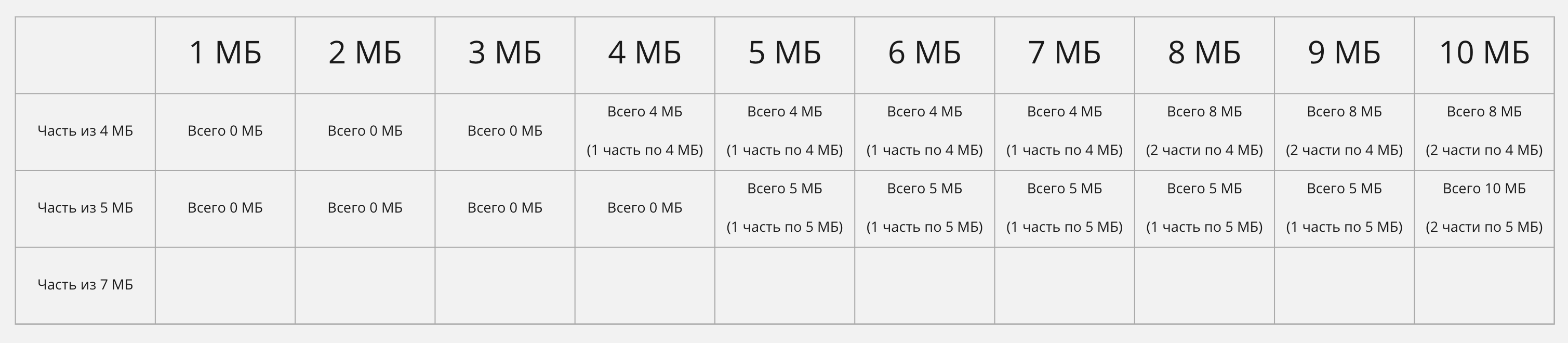
Но уже здесь мы видим неоптимальность. В 4 МБ всё ещё может поместиться одна часть по 4 МБ, в 8 МБ — две части. А вот в 9 МБ мы уже можем добавить части двух разных размеров и использовать все 9 МБ. Это обеспечит нам максимальную утилизацию пространства. Давайте обновим максимумы в нашей таблице с учётом решения предыдущей подзадачи!

По такому же принципу заполним и третью строку:

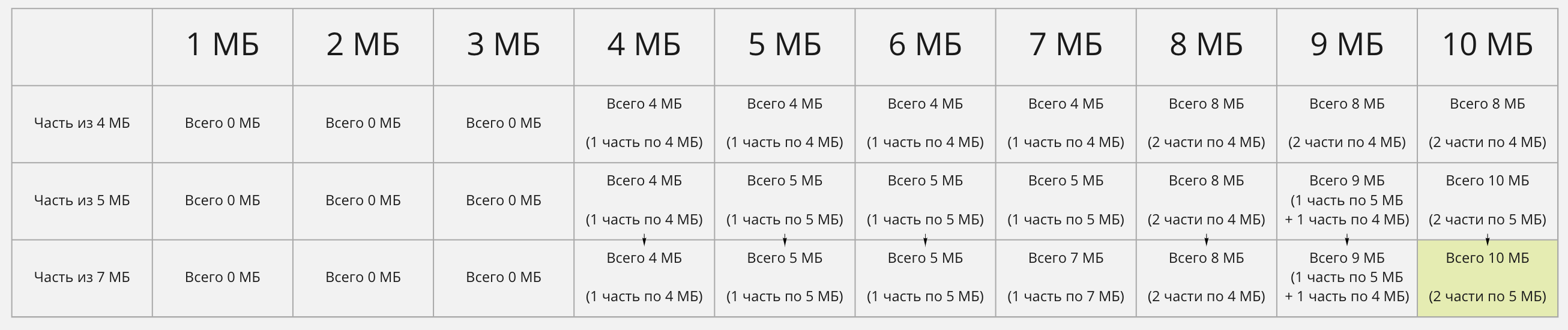
Теперь в нижней правой ячейке таблицы и есть решение нашей задачи! Это переиспользованное решение подзадачи с двумя предыдущими доступными частями.

Самое время формализировать алгоритм заполнения этой таблицы, ведь до этого момента мы пользовались лишь здравым смыслом. Алгоритм довольно простой: в каждую ячейку идёт максимум из двух значений. Первое — это максимум решения предыдущей задачи (то, что находится ровно над заполняемой ячейкой), если он есть. А второе — размер максимального количества частей, помещающихся в этот размер + максимум решения предыдущей задачи для оставшегося места, если он есть.

Например, когда мы заполняли решение задачи для частей двух разных размеров и пачки в 9 МБ, мы посчитали максимальное количество места, которое можем занять частями этого размера (получилась одна часть в 5 мегабайт). И у нас осталось ещё 4 МБ, которые мы можем заполнить. Поэтому мы пошли в предыдущий столбец и посмотрели, чем мы можем заполнить их: одной частью в 4 МБ. Всего получилось 9 МБ. Ещё мы взяли максимум решения предыдущей подзадачи, 8 МБ, и максимум из двух получившихся чисел — 9. Это и пошло в нашу максимальную оценку для этой подзадачи.

Эта таблица будет давать тот же ответ, если мы поменяем строчки местами или добавим части новых размеров. Можете построить подобные таблицы с новыми правилами вручную, чтобы убедиться в этом.

Осталось лишь переложить нашу логику в код, чем мы и займёмся в следующей демонстрации.